Вычисление амёб полиномов двух переменных
Амёба полинома многих комплексных переменных является диаграммой Рейнхардта множества его нулей в логарифмическом пространстве по каждой из переменных. Термин «амёба» впервые введён в известной монографии «Discriminants, resultants and multidimensional determinants» И. М. Гельфанда, М. М. Капранова и А. В. Зелевинского в 1994 году, где даны два конкурирующих определения амёбы полинома: аффинная (рис. 1) и компактифицированная (рис. 2) версии. Оба определения интересны только в размерности два и выше, поскольку амёба полинома одного переменного является конечным множеством, которое можно исследовать с помощью различных классических методов локализации корней полиномов.
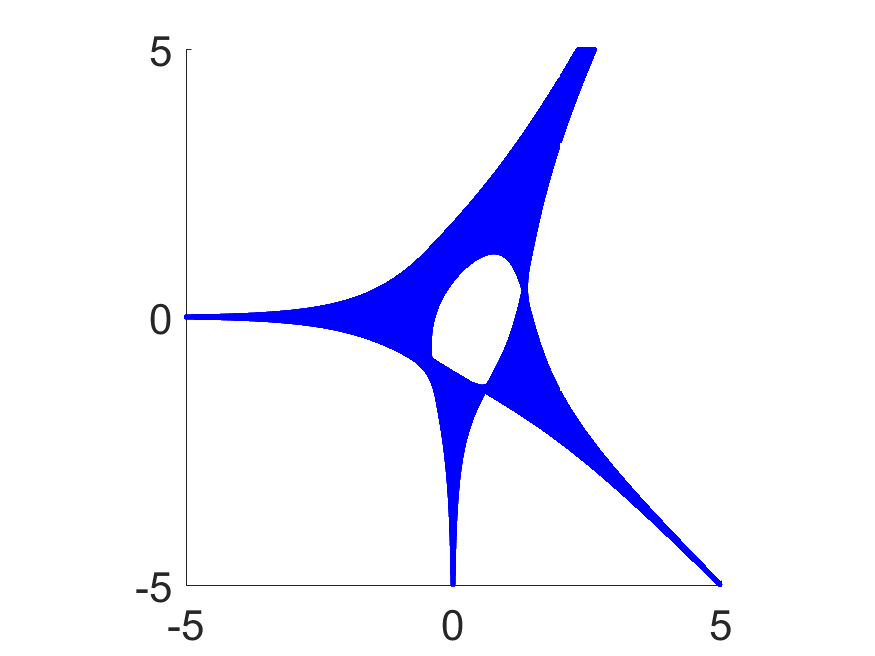
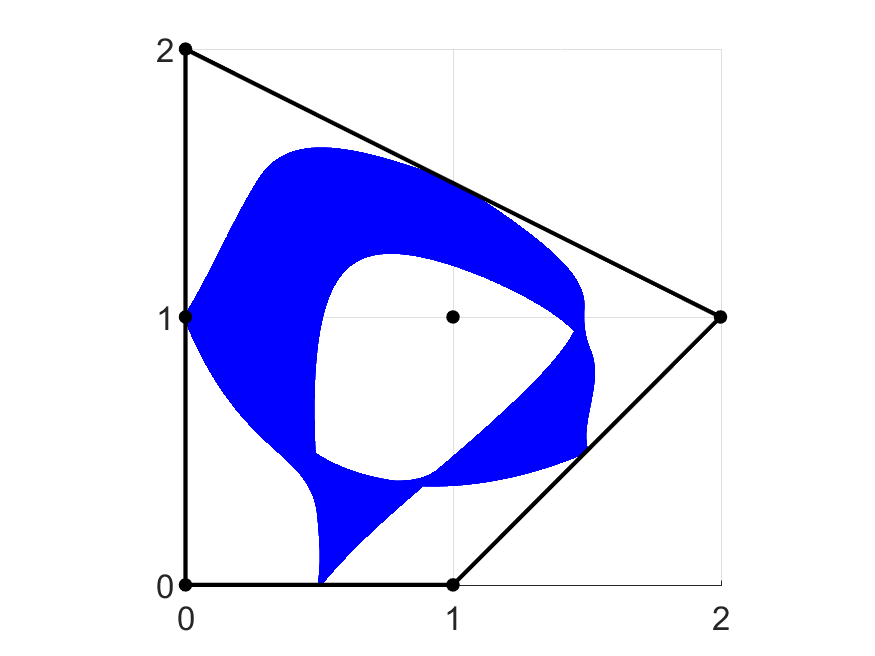
Геометрия амёбы полинома \(f(x) = \sum\limits_{\alpha\in A} c_\alpha x^\alpha \) содержит важную информацию о нулях этого полинома и тесно связана с комбинаторной структурой его многогранника Ньютона \(\mathcal{N}_{f}\). Несмотря на потерю половины вещественных размерностей, изображение множества нулей полинома в пространстве амёбы отражает относительный размер некоторых его коэффициентов.
Определение 1. Амёба \(\mathcal{A}_{f}\) полинома Лорана \(f\left(x\right)\) (или алгебраической гиперповерхности \(\left\{ f\left(x\right)=0\right\} )\) есть образ гиперповерхности \(f^{-1}\left(0\right)\) в пространство \[{\rm Log}:\left(x_{1},\ldots,x_{n}\right)\mapsto\left(\ln\left|x_{1}\right|,\ldots,\ln\left|x_{n}\right|\right).\]
Определение 2. Компактифицированная амёба \(\overline{\mathcal{A}}_{f}\) полинома Лорана \(f\left(x\right)\) (или алгебраической гиперповерхности \(\left\{ f\left(x\right)=0\right\} )\) есть образ гиперповерхности \(f^{-1}\left(0\right)\) относительно моментного отображения в многогранник Ньютона \(\mathcal{N}_{f}\): \[\left(x_{1},\ldots,x_{n}\right)\mapsto\frac{\sum\limits _{\alpha\in A}\alpha\cdot\left|x^{\alpha}\right|}{\sum\limits _{\alpha\in A}\left|x^{\alpha}\right|}=\frac{\sum\limits _{\left(\alpha_{1},\ldots,\alpha_{n}\right)\in A}\left(\alpha_{1},\ldots,\alpha_{n}\right)\cdot\left|x^{\alpha_{1}}_1\cdot\ldots\cdot x^{\alpha_{n}}_n\right|}{\sum\limits _{\left(\alpha_1,\ldots,\alpha_{n}\right)\in A}\left|x^{\alpha_{1}}_1\cdot\ldots\cdot x^{\alpha_{n}}_n\right|}.\]
Подробнее...Данный скрипт позволяет генерировать код программы для MatLab R2017a, которая вычисляет и отображает амёбу полинома \(f\left(x,y\right)\) двух комплексных переменных \(x\) и \(y\). Более подробно о работе алгоритма можно прочитать в статье Algorithmic computation of polynomial amoebas.
Amoeba of 1 + x + y + 4 x y + y^2 + x^2 y=0