Задание №1702/18

Обозначим через \( P\left(x, y\right) \), \( Q\left(x, y\right) \) и \( A\left(x, y\right) \) условия, что \(\left(x,y\right)\in \text{P}\), \(\left(x,y\right)\in \text{Q}\) и \(\left(x,y\right)\in \text{A}\) соответственно, после чего упростим исходное выражение, используя законы логики: \[Q\rightarrow A\lor P \Rightarrow A\lor P \lor \lnot Q.\]

Решение задачи имеет вид: \[A_{\min} = \lnot \left( P \lor \lnot Q \right) \Rightarrow \lnot P \wedge Q.\]

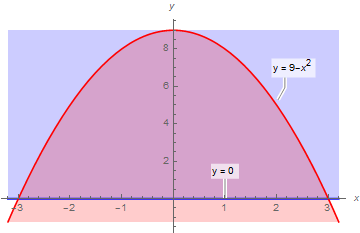
Таким образом, точка \(\left(x,y\right)\) принадлежит искомой области \(\text{A}_{\min}\) (см. рисунок 1) только в том случае, если одновременно выполняются два условия: \[y>0,\quad 9-x^{2}-y>0.\]

В силу симметрии достаточно рассмотреть лишь половину области, лежащую в первой координатной четверти. При \(x=1\) подойдут значения \(y=1,\ldots,7\), а при \(x=2\) подойдут значения \(y=1,\ldots,4\). Точки, лежащие на границе области, в решения не включаются, но следует однократно учесть точки, лежащие на оси ординат. При \(x=0\) подойдут значения \(y=1,\ldots,8\), следовательно, общее количество целых точек в области \(A_\min\) равно \(2\cdot(7+4)+8=30\).

Для получения изображения области \(\text{A}_{\min}\) (см. рисунок 1) использовалась следующая программа в среде Wolfram Mathematica 11.

Plot[{Callout[0, "y = 0", 1],
 Callout[9 - x^2, "y = 9 - x^2", 2]}, {x, -3.2, 3.2}, 
 Filling -> {1 -> Top, 2 -> Bottom}, AxesLabel -> {x, y}, 
 FillingStyle -> Automatic, PlotStyle -> {{Thick, Blue}, Red}]

30