Задание №1702/15

Задание

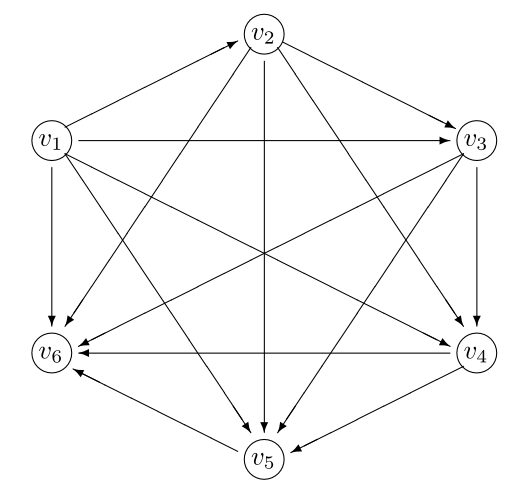
Схема дорог, связывающая \(n\) городов, имеет следующую структуру: из любого города \(v_{i}\) с номером \(1\leq i<n\) существует дорога в любой город \(v_{j}\), имеющий номер \(i<j\leq n\). По каждой дороге можно двигаться только в одном направлении — из города \(v_{i}\) в город \(v_{j}\) (на схеме показано стрелкой).

Пример такой схемы при \(n=6\) представлен на рисунке.

Сколько существует различных путей из города \(v_{1}\) в город \(v_{n}\), если \(n=10\)?

Решение

По индукции можно вывести формулу \(m=2^{n-2}\).

Подробнее...

Ответ

256

Подробнее...

© Д. В. Богданов, 2012–2018.