Задание №1702/04
Задание
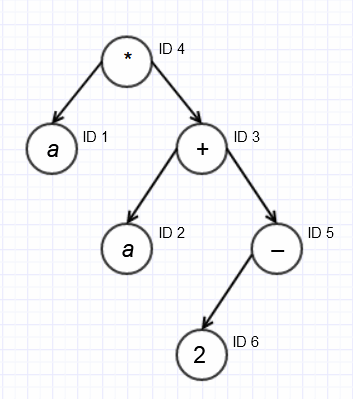
Во фрагменте базы данных сохранено дерево разбора некоторого арифметического выражения. На основании приведённых данных укажите значение a, при котором значение выражения будет наименьшим.
| ID | ID_родителя | Значение |
|---|---|---|
| 1 | 4 | a |
| 2 | 3 | a |
| 3 | 4 | + |
| 4 | 0 | * |
| 5 | 3 | – |
| 6 | 5 | 2 |
Решение
Построение дерева разбора арифметического выражения по имеющейся таблице подробно разобрано в решении задания 1701/04. Аналогичное дерево для данной таблицы представлено на рисунке 1. Таким образом, выражение имеет вид \(a*(a+(-2))\).
Согласно заданию, необходимо указать значение параметра \(a\), при котором выражение \(a\cdot(a-2)=a^2-2a\rightarrow\min\). Учитывая, что график выражения является параболой с ветвями, направленными вверх, точкой глобального минимума является вершина этой паработы \(a_\min=-\frac{-2}{2\cdot 1}=1\).
Альтернативный способ вычисления \(a_\min\) — применение понятия производной. Учитывая, что \(\left(a^2-2a\right)'=2a-2\), из необходимого условия существования экстремума получим \(2a-2=0\Rightarrow a=1\). Используя достаточное условие существования экстремума, легко убедиться, что найденная точка \(a=1\) является точкой минимума.
Подробнее...Ответ
1
Подробнее...- Комментариев пока нет...