Задание №1701/05

Для решения задачи воспользуемся алгоритмом Шеннона-Фано. Кодовые слова \(\gamma-0\) и \(\omega-10\) будем считать запрещёнными и не использовать в алгоритме. Таким образом, кратчайшим разрешённым кодовым словом является слово 11.

Оставшиеся символы \(\vartheta\), \(\xi\) и \(\chi\) имеют вероятности 0,25, 0,12 и 0,12 соответственно. Эти символы необходимо разделить на две группы таким образом, чтобы суммарные вероятности входящих в группы символов были максимально близки друг к другу. Если в первую группу выделить символ \(\vartheta\), а во вторую — \(\xi\) и \(\chi\), то суммарные вероятности символов первой и второй группы будут соответственно равны 0,25 и 0,12 + 0,12 = 0,24. В этом случае символ \(\vartheta\) получит кодовое слово 110, а кодовые слова символов второй группы будут начинаться на 111.

Но по условию задачи код для буквы \(\xi\) должен иметь наименьшее числовое значение, поэтому символу \(\vartheta\) лучше назначить код 111, а префикс 110 присвоить кодовым словам для символов \(\xi\) и \(\chi\). Стоит отметить, что после подобного обмена код останется префиксным и оптимальным по суммарной длине кодовых слов.

Повторяя шаги алгоритма, необходимо поделить на две группы оставшиеся символы \(\xi\) и \(\chi\). Очевидно, что в каждую из групп войдёт ровно один символ. Учитывая, что кодовое слово для \(\xi\) должно иметь минимальное числовое значение, из двух возможных кодовых слов 1100 и 1101 выберем первое.

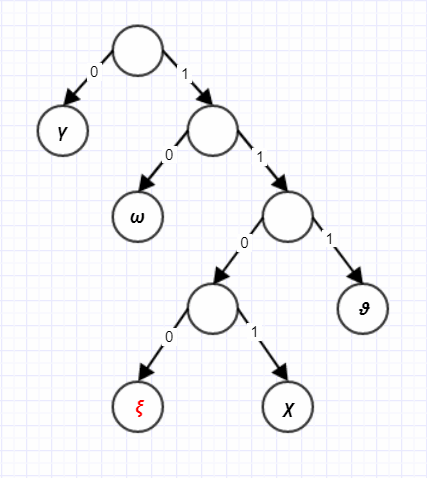
По построеному кодовому дереву (рисунок 1) легко убедиться, что полученный код является префиксным (все кодовые слова являются листьями этого дерева) и, следовательно, обладает свойством однозначного декодирования.

Важно отметить, что использование алгоритма Шеннона-Фано не гарантирует оптимальность кода по суммарной длине кодовых слов, хотя во многих случаях (в том числе, в данной задаче) получаемый код совпадает с оптимальным. Для вычисления оптимальных кодов можно использовать алгоритм Хаффмана.

1100